图

图涉及到很多基础概念，在离散数学里有讲，这里先简单介绍一下

• 图由顶点（vertex）和边（edge）组成，通常表示为 G = (V, E)
• G表示一个图，V是顶点集，E是边集
• 顶点集V有穷且非空
• 任意两个顶点之间都可以用边来表示它们之间的关系，边集E可以是空的

有向图

• 有向图的边是有明确方向的
• 有向无环图（Directed Acyclic Graph，简称 DAG）

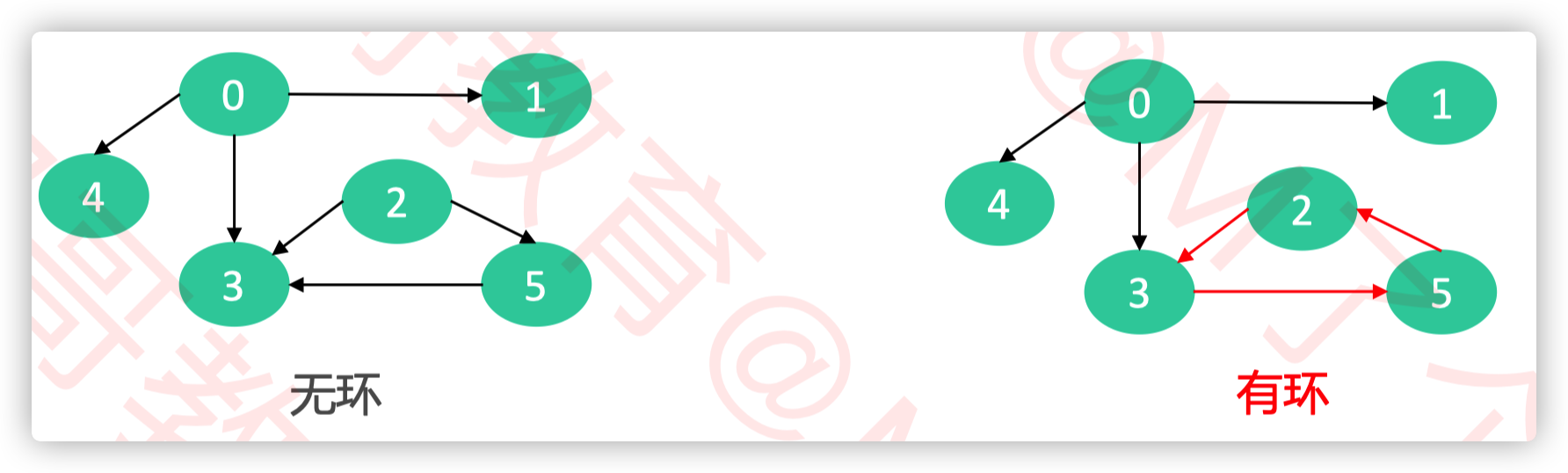
• 如果一个有向图，从任意顶点出发无法经过若干条边回到该顶点，那么它就是一个有向无环图

入度出度

• 出度、入度适用于有向图

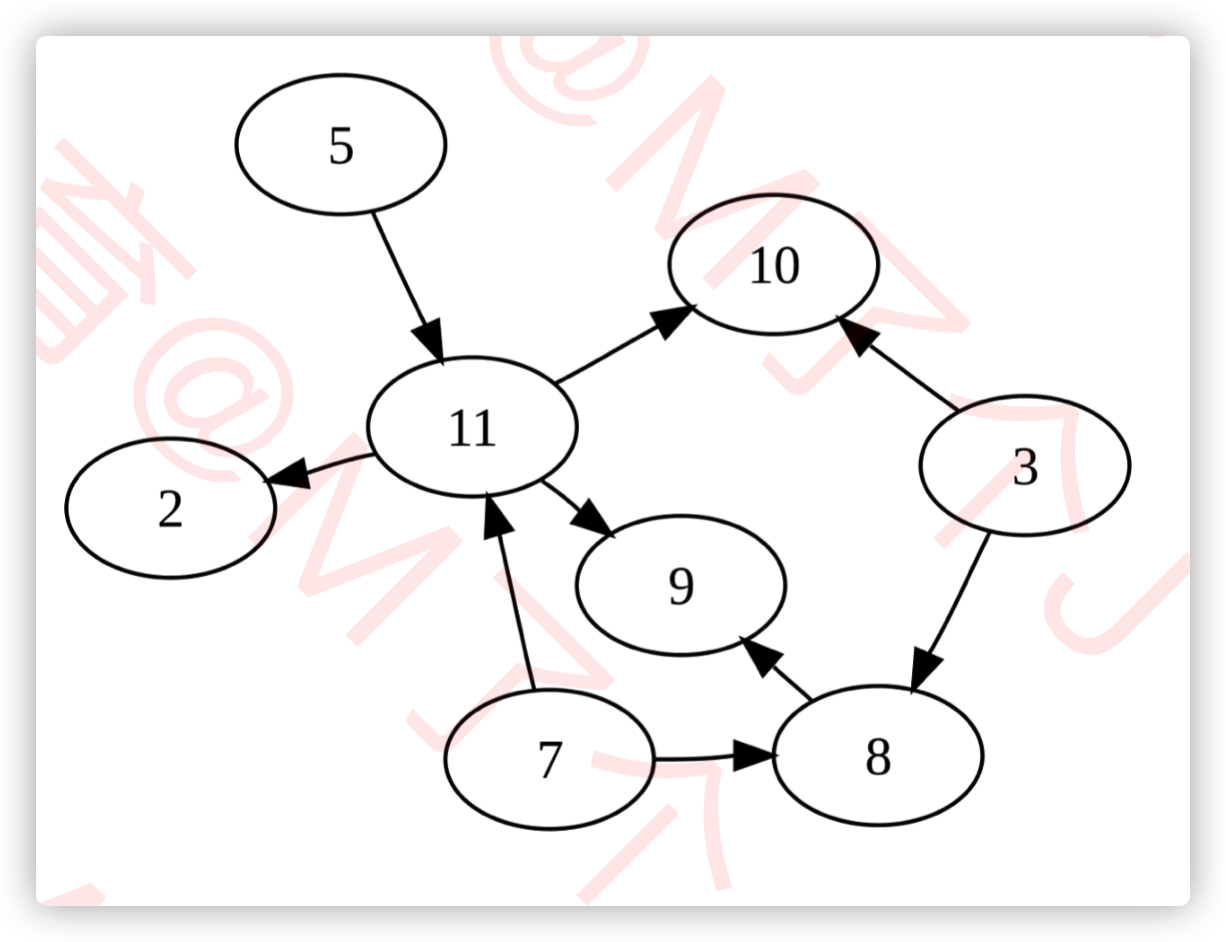
• 出度（Out-degree） 一个顶点的出度为 x，是指有 x 条边以该顶点为起点 如：顶点11的出度是3

• 入度（In-degree） 一个顶点的入度为 x，是指有 x 条边以该顶点为终点 如：顶点11的入度是2

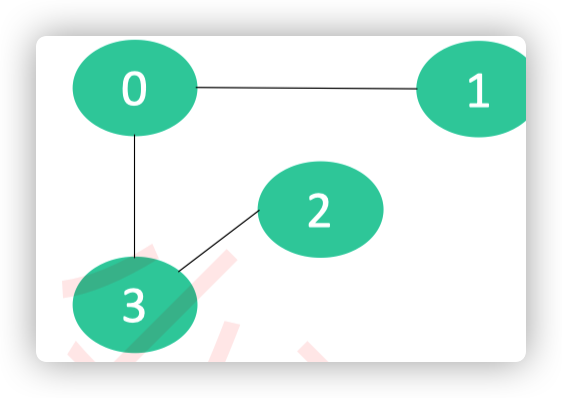
无向图

• 无向图的边是无方向的
• 可以把无向图的边看成是双向的有向边

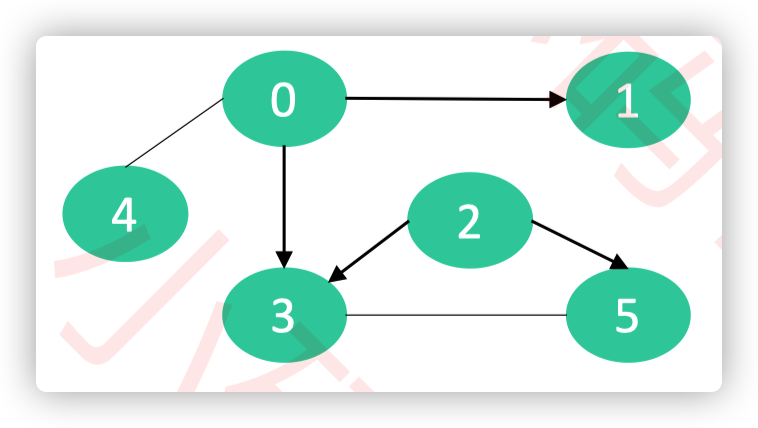
混合图

• 边可以是有向的也可以是无向的

简单图，多重图

平行边

• 在无向图中，关联一对顶点的无向边如果多于1条，则称这些边为平行边
• 在有向图中，关联一对顶点的有向边如果多于1条，并且它们的的方向相同，则称这些边为平行边

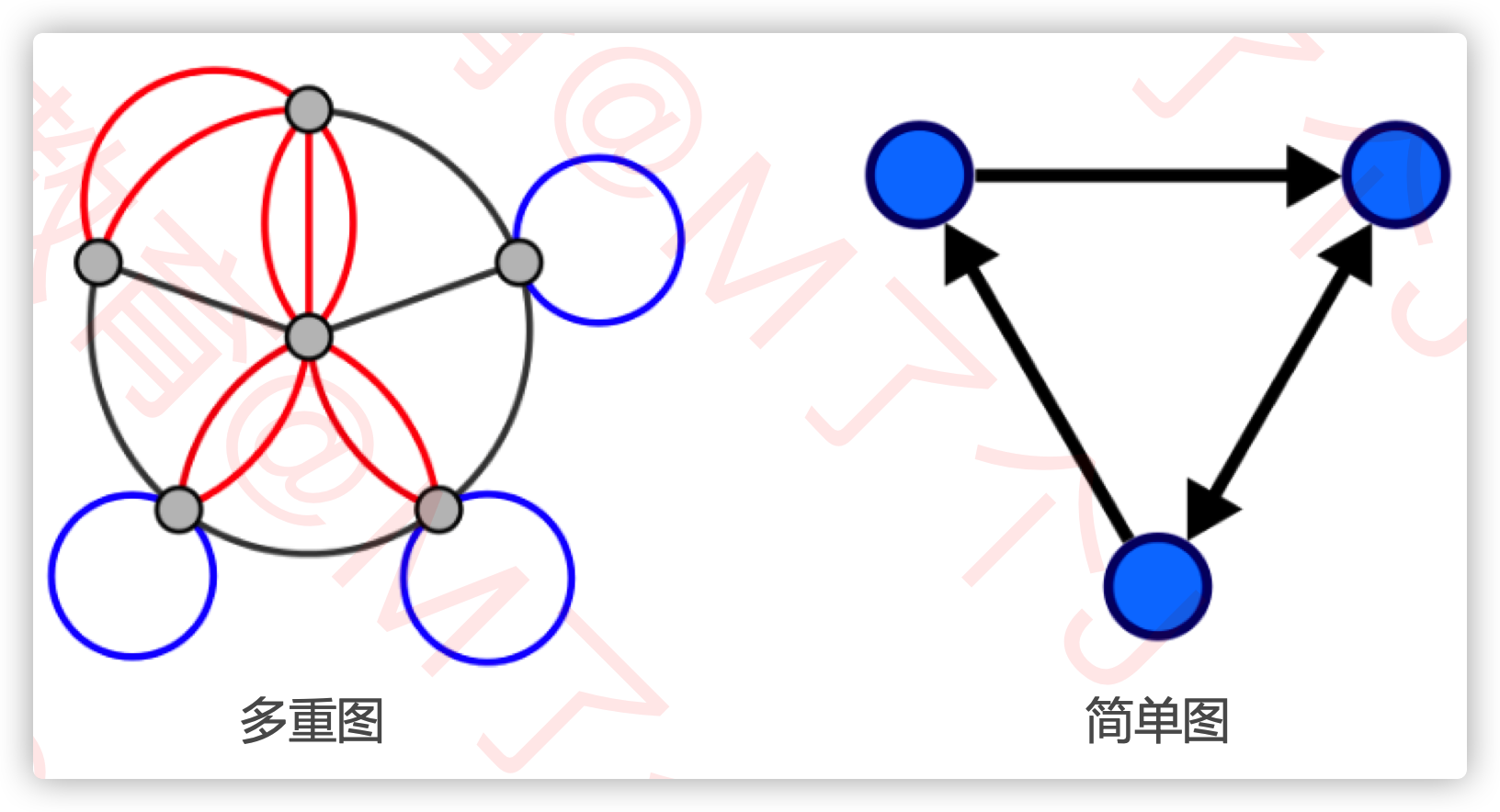
多重图

• 多重图（Multigraph） 有平行边或者有自环的图

简单图

• 既没有平行边也不没有自环的图

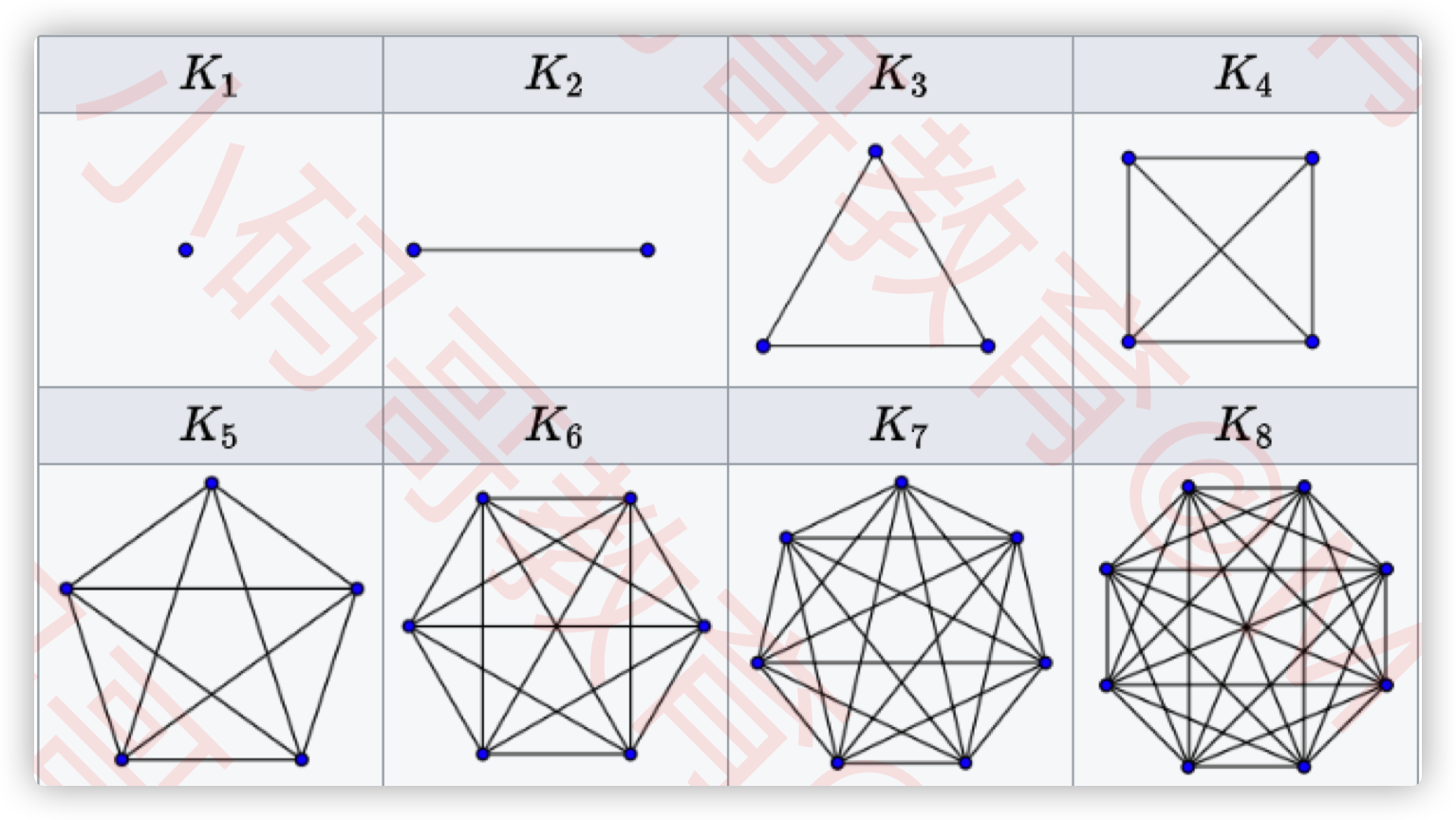
无向完全图

• 无向完全图的任意两个顶点之间都存在边

• n 个顶点的无向完全图有 n ( n − 1 )/ 2 条边

• n− 1 + n− 2 + n− 3 + ⋯ + 3 + 2 + 1

有向完全图

• 有向完全图的任意两个顶点之间都存在方向相反的两条边

• n 个顶点的有向完全图有 n ( n − 1 ) 条边

• 稠密图（Dense Graph）：边数接近于或等于完全图

• 稀疏图（Sparse Graph）：边数远远少于完全图

有权图

• 有权图的边可以拥有权值（Weight）