并查集

• 并查集也叫作不相交集合（Disjoint Set）

实际上并查集就是用数组来存储树形结构

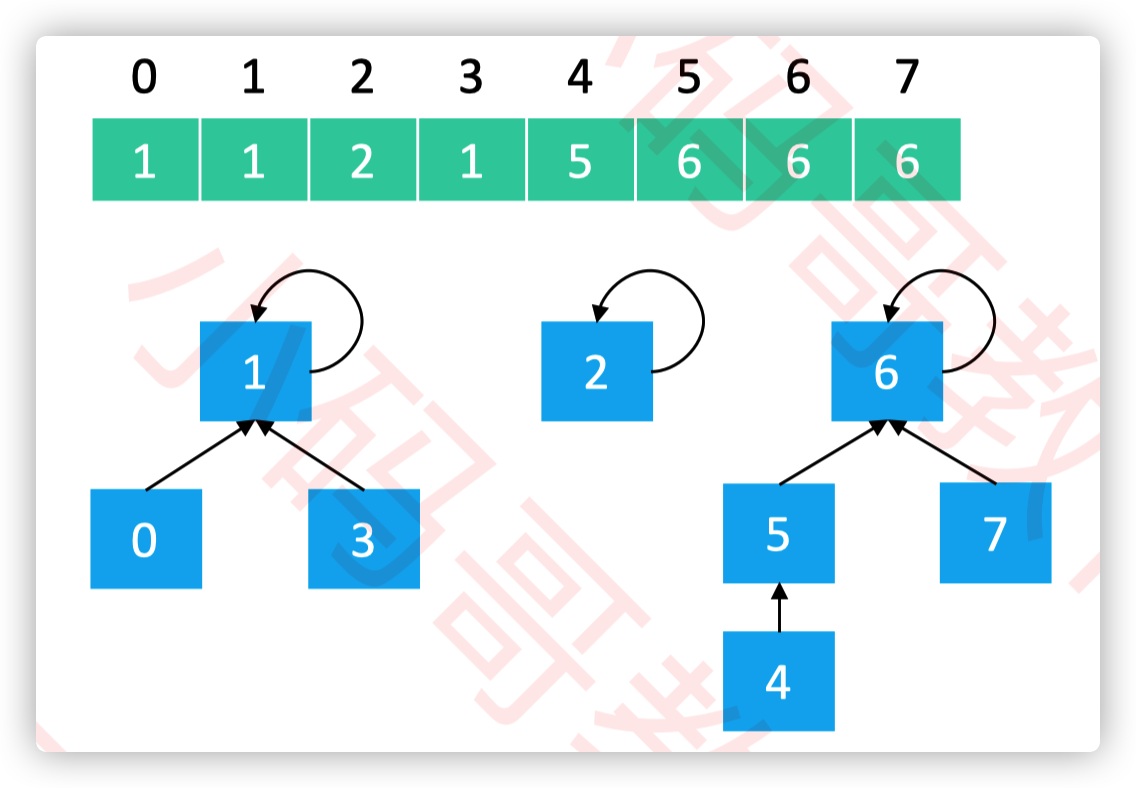
并查集有2个核心操作

• 查找（Find）：查找元素所在的集合（这里的集合并不是特指Set这种数据结构，是指广义的数据集合）
• 合并（Union）：将两个元素所在的集合合并为一个集合

有2种常见的实现思路

• Quick Find 查找（Find）

  操作	查找（Find）	合并（Union）
  时间复杂度	O ( 1 )	O ( n )

• Quick Union 查找（Find）的时间复杂度： O ( lo g n ) ，可以优化至 O 𝛼 𝑛

  合并（Union）的时间复杂度： O ( lo g n ) ，可以优化至 O 𝛼 𝑛， α ( 𝑛 ) < 5 ， α ( 𝑛 ) < 5

  操作	查找（Find）	合并（Union）
  时间复杂度	O ( lo g n )	O ( lo g n )

接口设计

public abstract class UnionFind {
    protected int[] parents;

    public UnionFind(int capacity) {
        if (capacity < 0) {
            throw new IllegalArgumentException("capacity must be >= 1");
        }

        parents = new int[capacity];
        for (int i = 0; i < parents.length; i++) {
            parents[i] = i;

        }
    }

    /**
     * 合并
     *
     * @param v1
     * @param v2
     */
    public abstract void union(int v1, int v2);

    public abstract int find(int v);

    /**
     * 判断v1，v2是否属于同一个集合
     * @param v1
     * @param v2
     * @return
     */
    public boolean isSame(int v1, int v2) {
        return find(v1) == find(v2
        );
    }

    protected void rangeCheck(int v) {
        if (v < 0 || v >= parents.length) {
            throw new IndexOutOfBoundsException("v is out of bounds");
        }
    }

}

QuickFind

• Quick Find 的 union(v1, v2)：让 v1 所在集合的所有元素都指向 v2 的根节点
• 因此需要遍历数组，时间复杂度O(n)
• Find(v)只需O(1)

public class UnionFind_QF extends UnionFind {


    public UnionFind_QF(int capacity) {
        super(capacity);
    }

    @Override
    public void union(int v1, int v2) {
        int p1 = find(v1);
        int p2 = find(v2);
        if (p1 == p2) {
            return;
        }

        for (int i = 0; i < parents.length; i++) {
            if (parents[i] == p1) {
                parents[i] = p2;
            }

        }
    }

    /**
     * 查找v所属的集合
     *
     * @param v
     * @return
     */
    @Override
    public int find(int v) {
        rangeCheck(v);
        return parents[v];
    }


}

QuickUnion

• union操作时只是将一侧节点指向另一个节点
• find操作时需要递归向上找到根节点

public class UnionFind_QU extends UnionFind {
    public UnionFind_QU(int capacity) {
        super(capacity);
    }

    @Override
    public void union(int v1, int v2) {
        int p1 = find(v1);
        int p2 = find(v2);
        if(p1==p2) {
            return;
        }
        parents[p1] = p2;

    }

    @Override
    public int find(int v) {
        rangeCheck(v);
        while (v!=parents[v]){
            v = parents[v];
        }
        return v;
    }
}

QuickUnion_S

• 可以看出，在QuickUnion中union操作时固定的将节点接到另一边可能导致树的高度很高，不利于find操作
• 可以根据节点所在集合中元素个数多少来决定将节点接到哪一边

public class UnionFind_QU_S extends UnionFind {
    private int[] sizes;

    public UnionFind_QU_S(int capacity) {
        super(capacity);
        sizes = new int[capacity];
        for (int i = 0; i < sizes.length; i++) {
            sizes[i] = 1;
        }
    }

    @Override
    public void union(int v1, int v2) {
        int p1 = find(v1);
        int p2 = find(v2);
        if (p1 == p2) {
            return;
        }

        if (sizes[p1] < sizes[p2]) {
            parents[p1] = p2;
            sizes[p2] += sizes[p1];
        } else {
            parents[p2] = p1;
            sizes[p1] += sizes[p2];
        }
    }

    @Override
    public int find(int v) {
        rangeCheck(v);
        while (v != parents[v]) {
            v = parents[v];
        }
        return v;
    }
}

QuickUnion_R

• 和上面的一样，但是根据树的高度进行判断

public class UnionFind_QU_R extends UnionFind_QU {

    //树高度数组
    private int[] ranks;

    public UnionFind_QU_R(int capacity) {
        super(capacity);
        ranks = new int[capacity];
        for (int i = 0; i < ranks.length; i++) {
            ranks[i] = 1;
        }
    }

    @Override
    public void union(int v1, int v2) {
        int p1 = find(v1);
        int p2 = find(v2);
        if (p1 == p2) {
            return;
        }
        if (ranks[p1] < ranks[p2]) {
            parents[p1] = parents[p2];
        } else if (ranks[p2] < ranks[p1]) {
            parents[p2] = parents[p1];
        } else {
            parents[p1] = parents[p2];
            ranks[p2] += 1;
        }
    }
}

• 虽然有了基于rank的优化，树会相对平衡一点

• 但是随着Union次数的增多，树的高度依然会越来越高 导致find操作变慢，尤其是底层节点（因为find是不断向上找到根节点）

union(1, 5)

• 什么是路径压缩？ 在find时使路径上的所有节点都指向根节点，从而降低树的高度

路径压缩

• 路径上的所有节点指向根节点

public class UnionFind_QU_R_PC extends UnionFind_QU_R {

    public UnionFind_QU_R_PC(int capacity) {
        super(capacity);
    }

    @Override
    public int find(int v) {
        rangeCheck(v);
        if (parents[v] != v) {
            parents[v] = find(parents[v]);
        }
        return parents[v];
    }
}

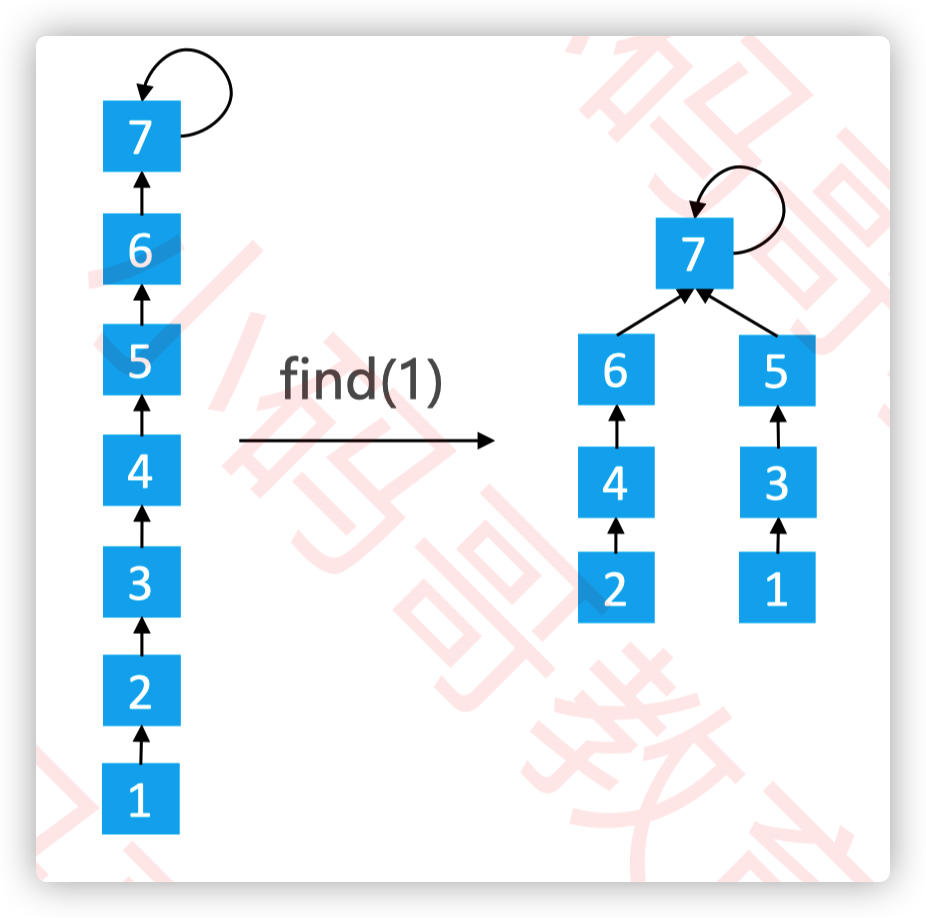
路径分裂

• 路径分裂：使路径上的每个节点都指向其祖父节点（parent的parent）

public class UnionFind_QU_R_PS extends UnionFind_QU_R {
    public UnionFind_QU_R_PS(int capacity) {
        super(capacity);
    }

    @Override
    public int find(int v) {
        rangeCheck(v);
        while (v != parents[v]) {
            int p = parents[v];
            parents[v] = parents[parents[v]];
            v = p;
        }
        return v;
    }
}

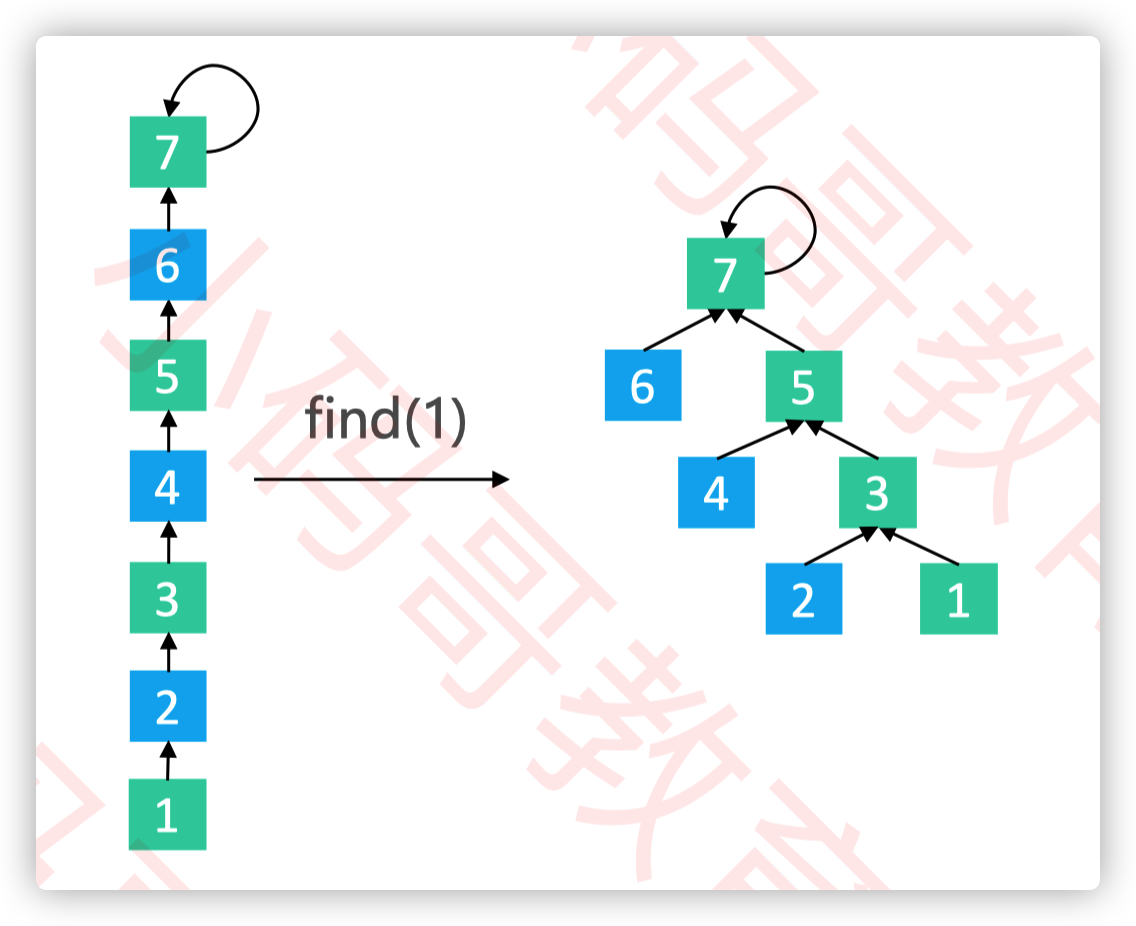
路径减半

• 路径减半：使路径上每隔一个节点就指向其祖父节点（parent的parent）

public class UnionFind_QU_R_PH extends UnionFind_QU_R {

    public UnionFind_QU_R_PH(int capacity) {
        super(capacity);
    }

    @Override
    public int find(int v) {
        rangeCheck(v);
        while (v != parents[v]) {
            parents[v] = parents[parents[v]];
            v = parents[v];
        }
        return v;
    }
}

泛型版本

public class GenericUnionFind<V> {
    private Map<V, Node<V>> nodes = new HashMap<>();

    public void makeSet(V v) {
        if (nodes.containsKey(v)) {
            return;
        }
        nodes.put(v, new Node<>(v));
    }

    /**
     * 找到根节点
     *
     * @param v
     * @return
     */
    private Node<V> findNode(V v) {
        Node<V> node = nodes.get(v);
        if (node == null) {
            return null;
        }
        while (!Objects.equals(node.parent.value, node.value)) {
            //路径减半
            node.parent = node.parent.parent;
            node = node.parent;
        }
        return node;
    }

    public V find(V v) {
        Node<V> node = findNode(v);
        return node == null ? null : node.value;
    }

    public void union(V v1, V v2) {
        Node<V> node1 = findNode(v1);
        Node<V> node2 = findNode(v2);
        if (node1 == null || node2 == null) {
            return;
        }
        if (Objects.equals(node1, node2)) {
            return;
        }
        if (node1.rank > node2.rank) {
            node2.parent = node1;
        } else if (node2.rank > node1.rank) {
            node1.parent = node2;
        } else {
            node1.parent = node2;
            node2.rank++;
        }
    }

    public boolean isSame(V v1, V v2) {
        return Objects.equals(findNode(v1), findNode(v2));
    }

    private static class Node<V> {
        V value;
        Node<V> parent = this;
        int rank = 1;

        public Node(V value) {
            this.value = value;
        }
    }
}

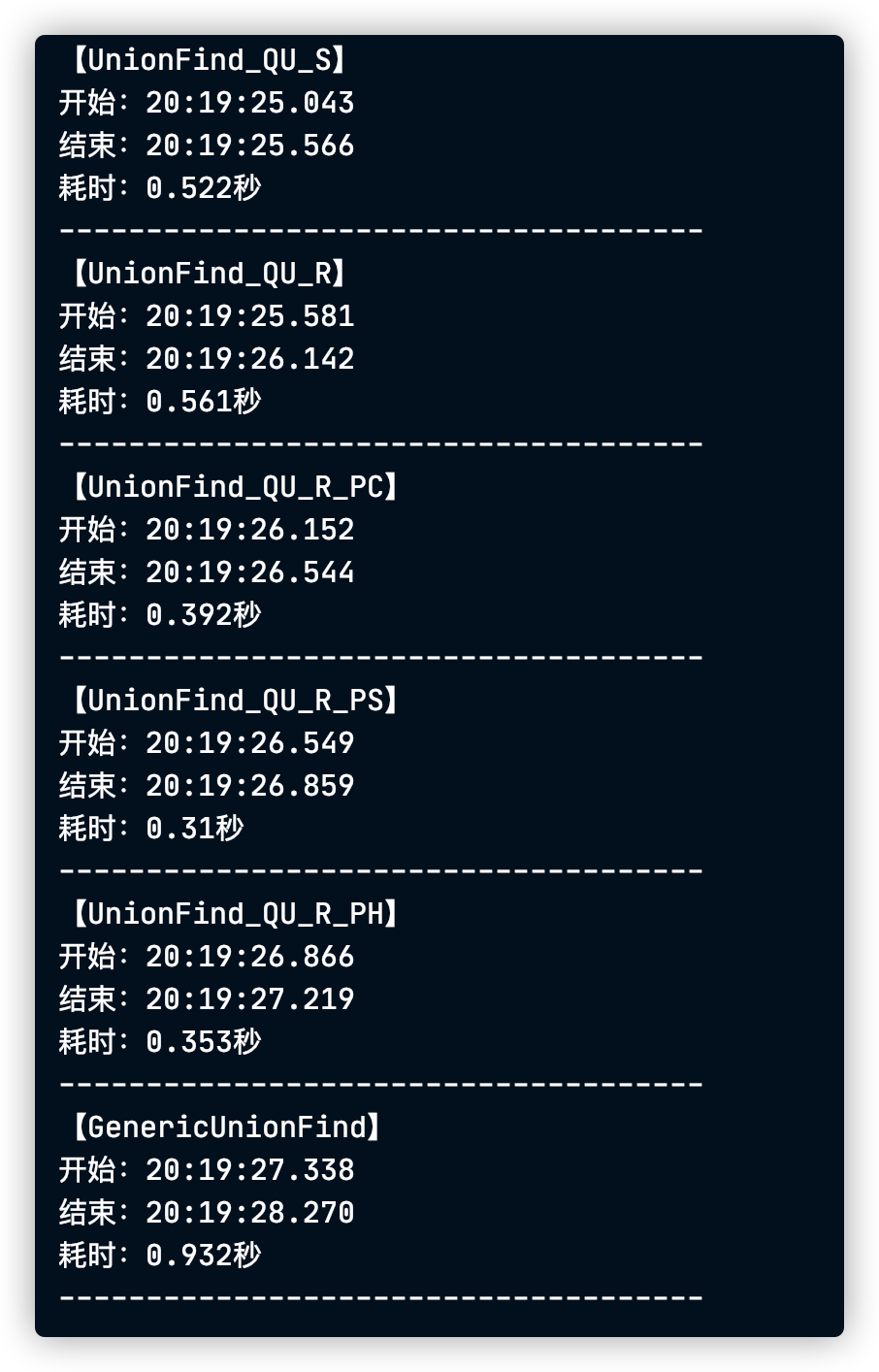
性能测试

• 100_0000数据